¿CÓMO DETERMINAR EL TAMAÑO DE LA MUESTRA PARA SU INVESTIGACIÓN?
¿CÓMO DETERMINAR EL TAMAÑO DE LA MUESTRA PARA SU INVESTIGACIÓN?
En la mayoría de los
trabajos de tesis y trabajos especiales de grado, desarrollado y financiado por
sus mismos autores, son precisamente los recursos económicos los menos
abundantes y a los que hay que ahorrar y hasta estirar para poder cubrir
exitosamente el trabajo de investigación planteado. De allí que se hace
imperioso para el equipo investigador trabajar con una muestra representativas
de su población objeto de estudio.
¿Cuáles son las razones para trabajar con una muestra?
En este instante surge la pregunta, por qué si cuento con toda la
población, está allí, estática, esperando para ser observada, estudiada,
entonces por qué debo tomar una muestra
para desarrollar la investigación para la tesis
de grado.
Las razones para tomar una
muestra y no observar a todos los componentes de la población objeto de
estudio siempre obedecen a razones de ahorro de recursos, ya sea de recursos
financieros o por ahorro de tiempo que es un recurso importante a tomar en
cuenta en el proceso de investigación. Así que el equipo investigador puede
encontrarse con que la población objeto de estudio:
-
Se encuentra muy dispersa en el ámbito
geográfico que se delimitó el estudio y cubrir a toda la población tomaría
mucho tiempo y acarrearía un gasto imposible de cubrir por el equipo
investigador.
-
O es una población cuyo acceso es peligroso y
cubrirla totalmente podría representar peligro para la integridad física de los
investigadores. Por ejemplo; personas que
viven en la calle o en vertederos de basura, zonas de alta peligrosidad
delictiva, gente relacionada con el tráfico y consumo de drogas, animales de
alta peligrosidad como fieras silvestres, o animales que habitan las profundidades
del mar o de lagos o internados en zonas inhóspitas, entre otros.
-
Puede ocurrir también que la población objeto es
escasa, se trata de minorías difícil de detectar y que además dispone de muy
poco tiempo para atender una entrevista como por ejemplo; músicos,
profesionales de la medicina u otra ciencia de la salud, pacientes de
enfermedades poco frecuentes, entre otros.
-
El muestro es destructivo, o más bien
la observación que se aplica sobre el elemento
de la muestra obliga a destruirlo, por lo tanto no es rentable destruir a
todos los elementos de la población para un estudio. Por ejemplo probar bombillos,
cauchos, zapatos o cualquier tipo de productos obliga a su uso y destrucción
por lo que se hace obligatorio trabajar con muestras
-
El fenómeno es continuo y nunca deja de ocurrir
por ejemplo; los accidentes tránsito que ocurren en un determinado sector de la
ciudad. Debe muestrearse por períodos de tiempo, la calidad de los productos
que sale de un proceso, las personas atendidas en un servicio, taquillas o
cajas de pago, auto lavados, pacientes odontológicos, etc.
Como se
puede apreciar, son muchas las situaciones en que un investigador puede
encontrarse, donde se hace imprescindible la utilización de Técnicas
de Muestreo para lograr cumplir exitosamente los objetivos de la
investigación.
¿Cuál es el tamaño de la muestra?
Para determinar correctamente el tamaño de la muestra y que esta sea una
muestra representativa de la población es necesario conoce varias cosas como la
distribución
de probabilidad que sigue la variable en estudio, el tamaño
de la población y el error máximo admisible.
- Para
la mayoría de los estudios sociales, a menos que se indique lo contrario, se
supone que la variable en estudio sigue una Distribución Normal, lo
que quiere decir que si la variable que se observa es numérica la mayoría de
los elementos de la población se encuentran concentrados alrededor de la media poblacional y a medida que los valores de la variables se alejan de la
media la población o frecuencia de individuos va disminuyendo, por ejemplo ingreso en unidades monetaria de los
hogares, peso y talla del bebé al nacer, distancia entre el hogar y el
lugar de trabajo de los empleados, estatura de los atletas que practican cierta
disciplina deportiva, etc.
- El Tamaño de la población. Una
población es una colección bien definida de objetos o individuos que tienen
características similares. Se pueden clasificar las poblaciones de dos tipos
bien definidos; la población objetivo, que suele tener diversas características
que son determinadas a hacer la delimitación del
estudio, la cual también es conocida como la
población teórica. La población accesible es la
población que realmente está al alcance del investigador y es sobre la cual los
investigadores aplicaran sus conclusiones.
- Margen de error (intervalo
de confianza). El margen de error es un estadígrafo
que expresa la cantidad de error de muestreo aleatorio en los
resultados de una encuesta, es decir, es la medida estadística del número de
veces de cada 100 que se espera que los resultados se encuentren dentro de un
rango específico. En los estudios sociales este error o nivel de significación
se ubica por general entre 5% y 10%, el valor más frecuentemente utilizado es
de 5%. Sin embargo en estudios médicos, farmacológicos donde podría ponerse en
riesgo la salud o integridad física del individuo observado, este error tiende
a ubicarse lo más pequeño posible, muy frecuentemente en 1%.
- Nivel de confianza. Son intervalos
aleatorios que se usan para acotar un valor con una determinada probabilidad
alta. Por ejemplo, un intervalo de confianza de 95% significa que los resultados
de una acción probablemente cubrirán las expectativas el 95% de las veces.
- La desviación estándar o desviación típica.
Es un índice numérico de la dispersión de un conjunto de datos (o
población). Mientras mayor es la desviación estándar, mayor es la dispersión de
la población.
¿Cómo se saca una muestra para una encuesta?
Calcular el tamaño de muestra Cuando se Desconoce el Tamaño de la Población
La fórmula para calcular el tamaño de muestra Cuando se Desconoce el Tamaño de la
Población es la siguiente:
En donde:
Z = nivel de confianza,
p = probabilidad de éxito, o proporción esperada
q = probabilidad de fracaso
d = precisión (error máximo admisible en términos de proporción)
Cálculo del Tamaño de la Muestra conociendo el Tamaño de la Población
La fórmula para calcular el tamaño de muestra cuando se conoce el tamaño
de la población es la siguiente:
En donde, N = tamaño de la población
Z = nivel de confianza,
p =
probabilidad de éxito, o proporción esperada
q = probabilidad de fracaso
d =
precisión (Error máximo admisible en términos de proporción).
EJEMPLOS DE CÁLCULO DEL TAMAÑO DE LA MUESTRA
Ejemplo: ¿A cuántas personas
tendríamos que estudiar para conocer la prevalencia de diabetes?
Seguridad = 95%; Precisión =
3%: Proporción esperada = asumamos que puede ser próxima al 5%; si no
tuviésemos ninguna idea de dicha proporción utilizaríamos el valor p = 0,5
(50%) que maximiza el tamaño muestral:
Donde:
Za 2 = 1,962 (ya que
la seguridad es del 95%) y se supone que la variable se distribuye normal
p = proporción
esperada (en este caso 5% = 0.05)
q = 1 – p (en
este caso 1 – 0.05 = 0.95)
d = precisión
(en este caso deseamos un 3%)
Si la población es finita, es
decir se conoce el total de la población y desea conocer cuántos del total se
tiene que estudiar la respuesta seria:
Donde:
N = Total de la
población
Za2 = 1.962 (si la
seguridad es del 95%)
p = proporción
esperada (en este caso 5% = 0.05)
q = 1 – p (en
este caso 1-0.05 = 0.95)
d = precisión
(en este caso deseamos un 3%).
¿A cuántas personas tendría
que estudiar de una población de 15.000 habitantes para conocer la prevalencia
de diabetes?
Seguridad = 95%;
Precisión = 3%;
proporción esperada =
asumamos que puede ser próxima al 5% ; si no tuviese ninguna idea de dicha
proporción utilizaríamos el valor p = 0.5 (50%) que maximiza el tamaño
muestral.
Según diferentes seguridades
el coeficiente de Za
varía, así:
Si la seguridad
Za fuese del 90% el coeficiente
sería 1,645
Si la seguridad
Za fuese del 95% el coeficiente
sería 1,96
Si la seguridad
Za fuese del 97.5% el
coeficiente sería 2,24
Si la seguridad
Za fuese del 99% el coeficiente
sería 2,576
OTROS
ARTÍCULOS DE INTERÉS
|
|
|
|
|
|










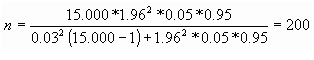







Comentarios
Publicar un comentario
Aquí puede comentar este artículo o enviar su mensaje directo a asesoriatesis60@gmail.com