¿QUÉ ES LA MATRIZ DE VESTER PARA LA PRIORIZACIÓN DE PROBLEMAS?
CÓMO UTILIZAR LA MATRIZ DE VESTER PARA LA PRIORIZACIÓN DE PROBLEMAS
En este artículo se expone a continuación una herramienta de
investigación que será de mucha utilidad en la jerarquización y priorización de
problemas a la hora de la formulación y evaluación de proyectos:
se trata de la Matriz de Vester. Desarrollada por el alemán Frederic
Vester (1925-2003), Esta matriz o diagrama permite
identificar las causas y efectos de una situación problemática. La
matriz Vester es un instrumento de desarrollo que forma parte de la
matriz del Marco Lógico.
Para entender mejor su utilidad, se puede imaginar estar en la situación
siguiente: Existe una problemática en la empresa (una petrolera) y se está
presentando un derrame de petróleo en un río. Para este problema puede haber
diversas causas y consecuencias, pero no se tiene conocimiento de cuál es la
causa raíz (la que desencadena otros problemas y efectos) ni tampoco la (o las)
principales consecuencias.
Es aquí cuando se decide utilizar la Matriz de Vester. Con ella se va
a determinar cuál es la principal causa (y con ello a priorizar los problemas) con base en los efectos que puede llegar a
ocasionar.
¿Qué es la matriz de Vester?
La matriz de Vester es, como toda matriz de vectores, una serie
de filas y columnas que muestran tanto horizontal (filas) como verticalmente
(columnas) las posibles causas (variables) de una situación problemática.
Entonces lo que se hace básicamente es confrontar los problemas
(variables) entre sí basándose en los siguientes criterios de calificación: 0,
1, 2 y 3, …, n
0: No lo causa
1: Lo causa indirectamente o
tiene una relación de causalidad muy débil
2: Lo causa de forma semi-directa
o tiene una relación de causalidad media
3: Lo causa directamente o
tiene una relación de causalidad fuerte
Otra calificación menos común preferida por otros autores e
investigadores es asignar valores de 1 a 5, como se puede ver en el artículo de
matriz de Vester de
Wikipedia. No obstante, por la experiencia adquirida en la aplicación de la
matriz
de Vester es suficiente con otorgar valores de 0 a 3, y es lo que se verá a
continuación.
La matriz de Vester en el análisis de problemas
El análisis de problemas es un punto a trabajar en el marco
lógico, razón por la cual la matriz de Vester es una
herramienta común en la metodología de marco lógico. ¿Y por
qué se dice esto?
Porque para explicar cómo realizar la Matriz de Vester,
es necesario mostrarte las herramientas que van de la mano con su aplicación, y
son herramientas que generalmente se trabajan con el enfoque de marco lógico.
Estas herramientas son la lluvia de ideas, árbol
de problemas, Diagrama de Causa-Efecto (espina de pescado), análisis
de Pareto, entre otras herramientas de análisis de problemas y que
permiten:
-
Capturar
los datos en torno a una situación problemática: Hoja de recolección de
datos
-
Plantear
los diferentes problemas: Cualquier método de generación de ideas
-
Caracterizar
y priorizar los problemas: Diagrama de pareto, diagrama causa y efecto,
matriz de Vester, árbol de problemas.
-
Definir
objetivos y plan de trabajo: Árbol de objetivos, diagrama de Gantt.
-
Trabajar
en la solución del problema cumpliendo los objetivos trazados.
Por lo tanto es necesario entender dónde se ubica la matriz de Vester
según el enfoque que se está mostrando. Con esto claro, se verá cómo
hacer la matriz de Vester.
Cómo hacer la matriz de Vester paso a paso
Determina las variables o problemas: A veces serán evidentes,
otras tendrás que recolectar datos que permitan determinar cuáles son los
posibles problemas. De todos modos, cualquier técnica de ideación como brainstorming, lluvia de ideas o Scamper,
le ayudará en su trabajo. No hay un número definido de cuántas ideas tener,
pues algunos autores creen que después de 13 problemas ya no son problemas y
otros creen que como mínimo requieres de 10 ideas para tener un resultado
decente. Sin embargo es aconsejable, investigar lo más que se pueda la
problemática, lo demás vendrá solo.
Redacta el problema: A
veces la forma en que se escribe solo es comprendida por quien lo escribe y
nadie más. Busque que los problemas queden redactados de tal forma que
cualquier persona que los lea, entienda que esto es un problema. Piense en el
impacto que esto ocasiona y no en el que está ocurriendo.
Por ejemplo:
Incorrecto: Faltan más máquinas que funcionen. Correcto:
Deficiente mantenimiento a la maquinaría.
Incorrecto: Falta más personal de servicio al cliente. Correcto:
Tiempo de espera muy largo para dar servicio al cliente.
Asigne un identificador al problema: Un id. Algo que permita
identificarlo fácilmente. Problema 1, problema 2, etc, o p1,..p2,…p3. Al final
del post encontrarás un formato en Excel de Matriz de Vester
y verá por qué es importante esto.
Ubique los problemas en la matriz: Tanto en la cabecera de
filas como de columnas. Si el enunciado del problema es muy largo, coloca su
código. Luego llena con 0 la diagonal principal, es decir, la coordenada donde
cada variable vertical concuerda con su homologo horizontal (1,1), (2,2),
(3,3), etc.
Califique las valoraciones: Asignar las ponderaciones
comenzando con el problema N° 1 de la fila versus el problema N° 2 de las
columnas. Las preguntas que te puedes hacer son:
¿Qué tanto puede llegar a
causar el problema N° 1 al problema N° 2?
¿Problema N° 1 causa
problema N° 2?
Una vez te haces la
pregunta, determina cuál es la relación de causalidad: ¿Es 1, 2 o 3? Recuerda
que no existe la misma relación de causalidad del problema N° 1 con respecto al
problema N° 2, comparada con el problema N° 2 con respecto al problema número N°
1. Por tal razón, esta matriz no es simétrica, es decir, una vez que asignes el
valor de (1,2), no vayas a ir a (2,1) y poner el mismo valor.
Ejemplo inicial de Matriz de Vester
Suma influencias y dependencias: en este punto ya tiene la
matriz diligenciada. Ok. Ahora se suman las filas y columnas. Lo que se obtiene de sumar cada fila se
conoce como la influencia/causa.
Es el nivel de influencia que tiene ese problema sobre otros. También
se conoce como motricidad. Por otra parte la suma de cada columna da el nivel de dependencia/efecto. Es el nivel en que un problema es causado
por otros.
Problemas
|
p1
|
p2
|
p3
|
p4.
|
p5
|
Pasivos
|
p1
|
0
|
3
|
3
|
2
|
1
|
9
|
p2
|
2
|
0
|
2
|
2
|
3
|
9
|
p3
|
2
|
1
|
0
|
1
|
2
|
6
|
p4
|
1
|
2
|
1
|
0
|
2
|
6
|
p5
|
2
|
2
|
1
|
1
|
0
|
6
|
Activos
|
7
|
8
|
7
|
6
|
8
|
36
|
Gráfica los problemas: En
el eje X se ubican los problemas activos, es decir aquellos con valores de la
influencia/causa. En el eje Y se colocan los problemas pasivos
(dependencia/efecto). Si el problema N° 2 tiene influencia 9 y dependencia 8,
pues su ubicación en el plano cartesiano será (9,8).
Clasifica los problemas:
Toma el mayor valor total de la suma que hiciste por filas y divídelo entre
dos. Haz exactamente lo mismo con el valor total de la suma con columnas. Con
los resultados, traza los ejes paralelos al eje x para los pasivos (suma por filas) y al eje y
para los activos (suma por columnas). Con esto obtendrás 4 cuadrantes:
Cuadrantes de matriz de Vester
Los problemas críticos tienen un total de activos y pasivos
altos. Son problemas causados por otros y a su vez son causados por los demás.
Debes tenerlos presentes en tu análisis
Los problemas pasivos tienen un alto total de pasivo y bajo
total de activo. Representan poca influencia causal. Al intervenir los
problemas activos, los pasivos deberían ser solucionados o mermados.
Los problemas indiferentes presentan un bajo total de activos y
pasivos, es decir, ni causan a otros ni son causados. Se consideran de baja
prioridad dentro del sistema analizado.
Los problemas activos se
encuentran en el cuarto cuadrante y presentan un alto total de activos y bajo
total de pasivos. No son causados por otros pero influyen mucho en los otros
criterios. Requieren atención y manejo crucial. Considéralos la causa principal
de la situación problemática.
Ejemplo de matriz de Vester
Se van a seguir los pasos descritos en el punto anterior. Este ejemplo se
trabajará solamente con 7 variables, aunque en la práctica real en muy probable
que se tengan muchas más, como antes se mencionó en el paso uno.
Resulta que los ciudadanos de una ciudad específica, Bruselas, están
investigando los problemas que tiene en su sistema de transporte colectivo:
El sistema de transporte de la ciudad de Bruselas, desde hace 6 meses
está reportando pérdidas mensuales por $ 50.000
El primer paso de la Matriz de Vester sería reunir a personas
claves en el caso, por ejemplo:
Expertos en sistemas de transporte
Ejecutivos que administran el sistema de transporte
Representantes de los usuarios del medio de transporte
Con estas personas, en una lluvia de ideas se obtuvo que:
ü
El tiempo de espera para abordar un bus es
demasiado alto
ü
Los buses se dañan en medio de la prestación del
servicio: Se quedan varados, tiene sonidos inusuales, pierden los frenos, etc.
ü
Hay sitios donde transitan muchas rutas pero hay
otros donde no llega ninguna
ü
En algunas zonas de la ciudad, es necesario
caminar mucho para llegar a un sitio donde pasa un bus
ü
Las personas se suben al bus sin pagar el pasaje.
ü
Hay una mala administración de la empresa
ü
El servicio no cuenta con la capacidad para
atender con calidad al número de usuarios de la ciudad
Como verás, estas solo son ideas surgidas en un ejercicio hipotético
hecho con el equipo de investigación pensando en el transporte de la ciudad
El segundo paso de la Matriz de Vester: estas ideas se deben
redactar como problema. El resultado es:
ü
Alto tiempo de espera para abordar el bus
ü
Deficiencia en el mantenimiento de los buses
ü
Mala planeación de las rutas del sistema de
transporte
ü
Cobertura insuficiente en el servicio prestado
por los buses
ü
Evasión del pago del pasaje al ingresar al bus
ü
Incorrecto manejo de los presupuestos del
sistema de transporte
ü
Capacidad insuficiente de servicio del sistema
de transporte
El tercero y cuarto paso de la Matriz de Vester: Le añadimos un
identificador a cada idea y comenzamos a crear la matriz. En ella colocamos
cero en la línea diagonal.
Hasta el momento, desde el paso uno hasta el paso cuatro de la
Matriz de Vester se lleva lo siguiente:
-
El ejemplo está desarrollado en una hoja
de cálculo en Excel muy fácil de hacer y que permitirá hacer las sumas
y operaciones algebraicas de manera automática, además se podrá utilizar en
otros casos que estudie en el futuro.
-
En el paso quinto, se asignará o calificará
enfrentando cada fila con cada columna. Enfrentamos Fila P1 con columna P2:
-
Y surge la interrogante: ¿El alto tiempo de
espera para abordar un bus causa la deficiencia en el mantenimiento de los
buses?
-
Se califica con 0, 1, 2 o 3 según se considere
con base en los criterios que te mencionaron iniciando el artículo. En este
caso, se podría asignar un cero (0). Porque se se aprecia relación entre uno y
otro.
-
Ora interrogante: ¿La mala planeación de las
rutas causa alto tiempo de espera para abordar un bus? Definitivamente sí.
Entonces, como aquí se confrontan la fila 3 con la columna 1, en (P3,P1) voy a colocar 3, porque lo causa
directamente.
-
Se hace este mismo procedimiento para cada celda
de la matriz llenando todos los campos haciéndose siempre la misma pregunta y
discutiendo entre todos porque si lo causa y porque no y qué tan directa o
indirectamente lo hace.
-
El paso siguiente es el paso seis, y aquí se va a
sumar las influencias (filas) y las dependencias (columnas).
-
Hasta aquí, el cálculo en la plantilla de Excel de la
matriz de Vester muestra el siguiente aspecto:
-
En el paso Siete se ubicarán los los
problemas en el plano cartesiano.
-
Así pues, P7 estará en la coordenada X = 6 Y = 3,
es decir (6,3). Haciendo exactamente el mismo procedimiento para cada suma
-
Ahora, en el paso ocho se va a clasificar los
problemas.
-
Seguidamente se identifica el problema que dio
un número más alto de activos (influencia) y lo vamos a dividir entre dos. En este
caso es 6 ya que P3, P6 y P7 dan 6, dividido por dos resulta 3. Se trazará una
recta paralela al eje Y en 3.
-
Haciendo lo mismo con los pasivos (dependencia)
obtenemos con valor máximo 10 por P1 y P4 lo que nos da 5 al dividirse entre 2,,
por lo tanto se traza una recta paralela al eje x en 5. Entonces se obtienen cuatro
cuadrantes, ya se tiene clasificación para todos los problemas. Como verás, es
la siguiente:
Problemas
pasivos: Cobertura insuficiente en el servicio prestado por los buses
Problemas
críticos: Deficiencia en el mantenimiento de los buses
Problemas
activos: Insuficiente capacidad de servicio del sistema de transporte e
Incorrecto manejo de los presupuestos del sistema de transporte
Problemas
indiferentes: Evasión del pago del pasaje al ingresar al bus
El
resultado hecho con el formato de la matriz de Vester en Excel es este:
Si te fijas, hay problemas que se encuentran atravesados por el eje de
clasificación. Es el caso de P2 y P5. Cuando esto ocurre, queda a juicio del
grupo su clasificación.
Clasificados los problemas, puede darse por finalizada la matriz de
Vester. Sin embargo no hay jerarquización de los problemas
Jerarquización de problemas
De la matriz de Vester al árbol de problemas
- Hay
varias herramientas que permiten analizar la relación entre un problema central
y sus causales. Diagrama de Ishikawa, matriz de Vester o el
árbol de problemas son sólo algunas de ellas. Unas permiten evidenciar
mejor que otras la jerarquización de problemas, y eso es lo que sea hará.
- La matriz de Vester elaborada en el
ejemplo anterior puede no ser suficientemente clara para quien recién conoce la
situación problemática, además en la clasificación de problemas que
esta otorga, no resulta evidente cuál es la relación entre los problemas.
- No vamos a detenernos a entender qué
es un árbol de problemas, para eso se tendrá un artículo aparte:
Cómo hacer un árbol de problemas
- Vamos a construir desde la matriz de Vester
un árbol de problemas:
- Elegimos uno de los problemas que se encuentran
en el cuadrante de los críticos. Normalmente el de puntuación más alta en
influencia y dependencia. Los otros problemas que se encuentren en este
cuadrante, serán las causas primarias al problema central elegido.
- Los problemas activos corresponden a las causas
secundarias o primarias en caso de que haya pocos o sólo un problema crítico.
- Las consecuencias o efectos son los problemas
pasivos.
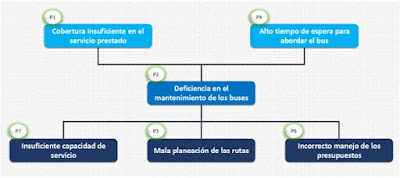
- Siguiendo estos tres pasos con el ejemplo de
transporte, el resultado es el siguiente:
Matriz de Vester from Ingenio Empresa
La metodología explicada es muy útil si se hace bien hecha, y merece
todo el esfuerzo posible, pues dentro de la planificación del proyecto, el
análisis y priorización de problemas supone una parte muy importante en el
éxito posterior del proyecto que estemos desarrollando.
Plantilla en Excel de la matriz de Vester
Con esta plantilla solo tendrás que escribir los elementos que van a
componer la matriz y definir su relación de causalidad tal como explicamos en
el post. Con esto tendrás listo el gráfico de la matriz de Vester y la
ubicación de los problemas en el cuadrante.
Si te gustó el artículo o tienes alguna crítica constructiva
coméntalo y recuerda suscribirte al
blog. Ah, y comparte con un Tiweet, +1 o por Facebook tus comentarios. Hasta
una próxima entrega.
OTROS ARTÍCULOS DE
INTERÉS
|
|
FUENTES BIBLIOGRÁFICAS Y DOCUMENTALES
Aguilo Alonso M.
Guia para la elaboración de estudios del Medio físico. Contenido y metodología,
Capítulo XIV, pg 647- 655. Madrid, 1993.
Cañedo Iglesias, Carlos
Manuel (2008) Estrategia Didáctica para Contribuir a la Formación de la Habilidad
Profesional Esencial “Realizar el Paso del Sistema Real al Esquema de Análisis”
en el Ingeniero Mecánico. Cuba- Universidad de Cienfuegos “Carlos Rafael Rodríguez
Chiimbila, Jojo
Cuthbert (s/f) Aplicación de la Matriz Vester. [Documento en línea] disponible
en: https://e-aulas.urosario.edu.co/.../Aplicación%20de%20la%20Matriz%20Vester.doc?...
[Consulta: 2018: julio 15]
Espinosa, G.
Gestión y fundamento de Evaluación de Impacto Ambiental. Banco Interamericano
de Desarrollo – BID. Centro de Estudios para el Desarrollo - CED, Santiago de Chile, 251pg, 2002.
Gómez Orea D.
Evaluación de Impacto Ambiental.2da edición. Editorial Agrícola Española, S.A.
Madrid, 1994.
Iingenioempresa.com
(2016) Matriz de Vester para la Priorización de Problemas [Documento en línea]
disponible en: https://ingenioempresa.com/matriz-de-vester/
[Consulta: 2018: julio 15]
















quién es el autor?
ResponderBorrar